Ao entrar no mundo do ROM hacking e da tradução de jogos, mais cedo ou mais tarde, você encontrará o conceito de hexadecimal. Diversos tutoriais orientarão o uso de um editor hexadecimal, mencionando que, para modificar e traduzir jogos, é necessário alterar os valores apresentados em hexadecimal.
O hexadecimal não é uma linguagem de programação nem uma linguagem de máquina. Trata-se simplesmente de um sistema numérico que, em nosso contexto, é empregado por ser a maneira mais eficaz de representar, visualizar e comunicar bits de forma compacta e legível. Não compreendeu a referência aos bits? Não se preocupe; essa compreensão virá mais adiante, após entender o hexadecimal como sistema numérico.
O objetivo deste tutorial é ser sua introdução aos números hexadecimais, permitindo que você explore mais profundamente o universo da modificação de jogos (e outros arquivos).
Antes de entender o sistema hexadecimal, precisamos refletir sobre o que são sistemas numéricos, começando pelo que estamos mais acostumados a utilizar no dia a dia: O sistema decimal.
Sistema decimal
Os números que usamos no dia a dia estão baseados no que é chamado de sistema decimal. Isso significa que utilizamos dez algarismos (de 0 a 9) para representar todos os números. O sistema decimal também é conhecido como sistema de base 10.
Sendo apenas dez algarismos para representar basicamente qualquer valor, o que fazemos quando eles se esgotam?
Começamos contando do 0 ao 9, usando os dez algarismos disponíveis. Quando chegamos ao 9 e queremos representar um número maior, adicionamos 1 à posição imediatamente à esquerda e zeramos a posição atual. Isso nos dá o número 10. E assim seguimos: 11, 12, 13, 14…
Isso continua indefinidamente à medida que os números aumentam. Ao chegar ao 99 e querer adicionar mais um, voltamos a zero na posição das unidades e das dezenas e adicionamos 1 à posição das centenas, resultando em 100.
Por mais óbvio que isso pareça, essa reflexão é importante para nos levar à dedução de que poderíamos fazer o mesmo com outra base ou com outra quantidade de algarismos! E se só existissem dois algarismos, ao invés de dez?
Imagine que, em uma realidade paralela, os algarismos como 2, 3, 4 e do 5 em diante não foram inventados. Criaram apenas o 0 e o 1.
Para representar o zero, usamos o 0. Para representar uma unidade, usamos o 1. E depois? Paramos de contar?
Não! Podemos usar a mesma lógica usada no próprio sistema decimal. Já que os algarismos acabaram, posso colocar um à esquerda para representar a base.
Neste caso, eu poderia representar duas unidades como 10, três unidades como 11. Acabou de novo? Tudo bem, colocamos mais um algarismo à esquerda e representamos quatro unidades como 100, cinco unidades como 101, seis unidades como 110, e assim por diante.
Conseguiu compreender?
E se eu lhe disser que essa realidade paralela, onde só temos dois algarismos, realmente existe? É o que chamamos de sistema binário.
Mas falaremos mais sobre ele em outra ocasião. A conclusão que precisamos tirar agora é que os números com os quais estamos acostumados a usar estão no sistema decimal e que podemos usar a mesma lógica para criar e utilizar outros sistemas que não sejam de dez algarismos.
Sistema hexadecimal
Após a introdução sobre o sistema decimal, entender a essência do sistema hexadecimal se torna mais simples. Basicamente, neste sistema, usamos dezesseis algarismos, ao invés de dez, para representar todos os números.
Hexadecimal: Sistema numérico que utiliza dezesseis algarismos. Também é conhecido como sistema de base 16.
Usamos os algarismos de 0 a 9 como de costume. No entanto, após o 9, em vez de adicionar um algarismo à esquerda como no decimal, introduzimos novos algarismos, que são as letras de A a F.
Para visualizar melhor, vamos contar em hexadecimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Agora sim, esgotaram-se os algarismos! Já sabemos o que fazer para continuar: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, e assim por diante.
Isso significa que, no sistema hexadecimal, “10” não representa dez unidades, mas sim dezesseis unidades. As dez unidades são representadas pelo algarismo “A”.
Veja uma tabela contendo números em hexadecimal, seu equivalente em decimal e quantas unidades cada número representa:
| Hexadecimal | Decimal | Valor |
|---|---|---|
| 00 | 0 | zero |
| 01 | 1 | um |
| 02 | 2 | dois |
| 03 | 3 | três |
| 04 | 4 | quatro |
| 05 | 5 | cinco |
| 06 | 6 | seis |
| 07 | 7 | sete |
| 08 | 8 | oito |
| 09 | 9 | nove |
| 0A | 10 | dez |
| 0B | 11 | onze |
| 0C | 12 | doze |
| 0D | 13 | treze |
| 0E | 14 | catorze |
| 0F | 15 | quinze |
| 10 | 16 | dezesseis |
| 11 | 17 | dezessete |
| 12 | 18 | dezoito |
| 13 | 19 | dezenove |
| 14 | 20 | vinte |
| 15 | 21 | vinte e um |
| 16 | 22 | vinte e dois |
| 17 | 23 | vinte e três |
| 18 | 24 | vinte e quatro |
| 19 | 25 | vinte e cinco |
| 1A | 26 | vinte e seis |
| 1B | 27 | vinte e sete |
| 1C | 28 | vinte e oito |
| 1D | 29 | vinte e nove |
| 1E | 30 | trinta |
| 1F | 31 | trinta e um |
Nomenclatura do hexadecimal
Ao trabalhar com sistemas numéricos, como você já viu, podemos encontrar um problema: Como saber a diferença entre “10” no sistema decimal (representa o valor “dez”) e “10” no sistema hexadecimal (representa o valor “dezesseis”), se os dois são escritos da mesma forma, mas representam valores diferentes?
Para isso, existem nomenclaturas para indicar que estamos representando números hexadecimais (e muitas destas nomenclaturas serão usadas dentro das linguagens de programação que você trabalhará).
Em muitos contextos, para evitar confusões, é comum utilizar um prefixo ou um formato especial para indicar claramente que estamos lidando com um número hexadecimal. Por exemplo, se eu lhe mostrar o número “0x10”, o prefixo “0x” é um sinalizador comumente aceito para mostrar que o número é hexadecimal. Portanto, “0x10” não é dez, como estamos acostumados a ver no nosso sistema decimal. Em vez disso, representa dezesseis unidades!
Outra nomenclatura popular, especialmente em design e programação web, é o uso do símbolo “#”. Quando vemos algo como “#10”, em contextos como seletores de cores CSS, sabemos que estamos lidando com um valor hexadecimal.
Então, ao ver “10” isoladamente, como saberíamos qual é a base? Em muitos casos, depende do contexto. Mas, usando prefixos claros como “0x” ou símbolos como “#”, eliminamos as dúvidas e tornamos nossa comunicação mais clara.
Veja o número hexadecimal “1F” em várias das nomenclaturas usadas para deixar claro que se trata de um valor hexadecimal:
- 0x1F
- #1F
- $1F
- 1Fh
- %1F
- &H1F
Nesta lista, as três primeiras são as mais usadas.
Outro ponto importante de salientar é que é comum colocar um “0” na frente quando estivermos representando os números de #0 a #F (veja que aqui já estou usando uma nomenclatura!). Na maioria das vezes, ao invés de usar, por exemplo, #5, escrevemos #05. Ao invés de #B, escrevemos #0B.
No contexto da computação, sempre usamos múltiplos de dois dígitos. Então, da mesma forma, ao invés de #1AF (três dígitos), complementamos com um 0 a esquerda, ficando #01AF (quatro dígitos, mesmo que o zero não interfira em nada no valor).
##Hexadecimal no cotidiano
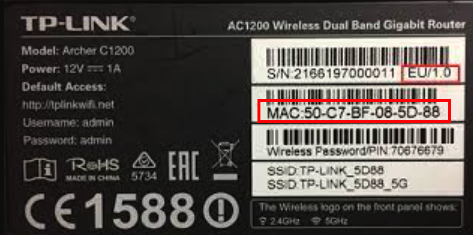
No nosso dia a dia, encontramos valores em hexadecimal sem perceber. Por exemplo, o MAC Address na etiqueta do seu roteador, frequentemente necessário para certas configurações, é um número hexadecimal.
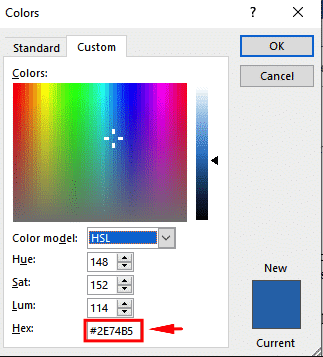
Além disso, ao definir cores em sites e designs web, usamos códigos hexadecimais. Quando você vê códigos como #FF0000, está observando uma representação hexadecimal para a cor vermelha. Esse sistema permite especificar uma vasta gama de cores de forma precisa e é amplamente utilizado no desenvolvimento web.
Você compreenderá o porquê disto, assim como aprenderá a interpretar estes números na medida que aprender mais sobre o assunto.
Conversão de hexadecimal
Se você estudar isto na faculdade, possivelmente o professor ensinará processos de conversão manual, passará exercícios e até mesmo exigirá que você faça conversão de decimal para hexadecimal e vice-versa em uma prova. Na prática, o que você precisa mesmo é entender o fundamento dos diferentes sistemas numéricos.
Com estes conceitos bem enraizados, você simplesmente sabe que #0A representa o valor “dez”, #0B representa “onze” e assim por diante. Muitos valores se repetem constantemente na prática. Por exemplo, na computação, trabalhamos muito com valores em hexadecimal de dois dígitos. Então, acabamos memorizando que #FF significa 255 em decimal. Memorizamos também que #10 em hexadecimal representa 16 em decimal.
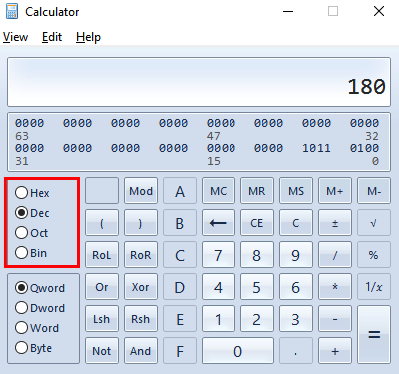
As calculadoras do Windows e do Mac possuem o modo Programação, e nele é possível realizar a conversão de diferentes sistemas numéricos.
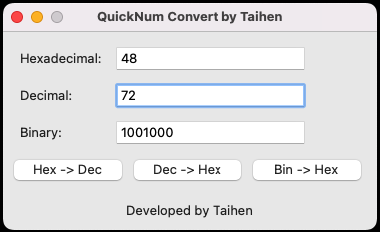
Eu também desenvolvi uma rápida ferramenta de conversão de sistemas, chamada QuickNum Converter. Nela, basta digitar um valor em um dos campos referentes aos sistemas numéricos e pressionar Enter para ver o mesmo valor convertido para os demais sistemas.
O próprio Google também pode fazer isso por você. No exemplo abaixo, eu digitei “convert 12 to hexadecimal” na barra de pesquisa.
O editor hexadecimal com outros olhos Agora podemos olhar para um editor hexadecimal com outros olhos. Na imagem abaixo, estamos verificando a memória da CPU de um jogo de NES que está sendo executado no emulador FCEUX.
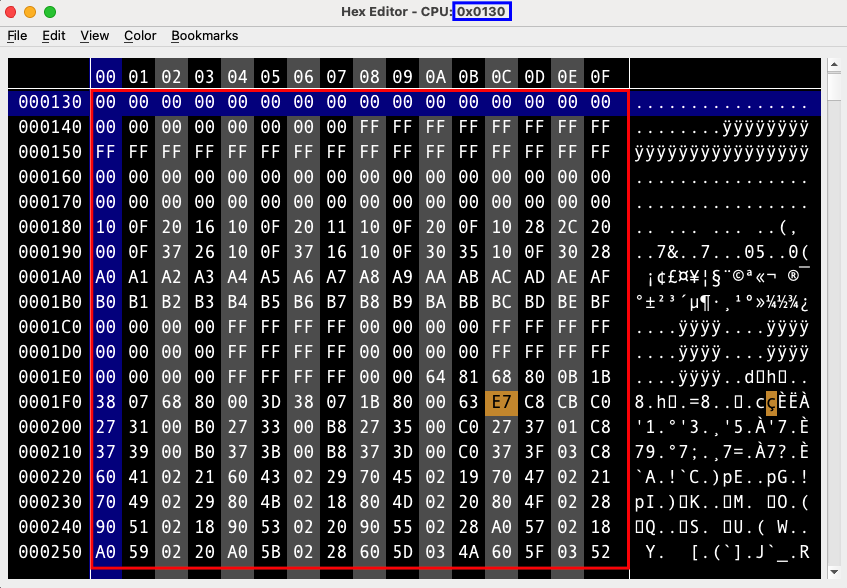
Destacado em azul no topo, temos um endereço de memória, também chamado de offset. Esse é um valor em hexadecimal, e você pode inclusive reconhecer uma das nomenclaturas que aprendeu neste tutorial.
Na região destacada em vermelho, podemos deduzir que se tratam de valores em hexadecimal, todos com dois dígitos. Você já teria até condições de pegar cada um deles e determinar o valor equivalente em decimal. Ou seja, o que estamos observando no editor são simplesmente números, porém em um sistema numérico diferente do que estamos acostumados (o sistema decimal).
Agora, podemos começar a questionar: Por que eles estão ali? Esses valores estão sendo usados para representar bits, que são a menor unidade de informação em computação e sistemas digitais. Refere-se ao famoso zero ou um, sobre o qual talvez você já tenha ouvido falar. Utilizar o sistema hexadecimal é uma excelente forma de compactar a exibição desses bits, tornando-os mais legíveis para nós.
Daqui para frente, não é possível aprofundar mais sem que você aprenda sobre o sistema binário e alguns conceitos fundamentais de eletrônica digital. Contudo, saiba que, ao observar esses valores no editor hexadecimal, você está praticamente vendo sinais elétricos!


